En esta página pondremos las respuestas a las diferentes preguntas que haremos en nuestra página de FACEBOOK, de la materia de admisión UNAM en Matemáticas.
Curso de Matemáticas Admisión UNAM.
Te invito a nuestro curso que iniciará el próximo lunes 11 de enero
Me puede enviar un WHATSAPP mediante el siguiente link:
Mensaje WHATSAPP para informes de curso de matemáticas clic aquí
o al siguiente celular un mensaje o llamada:

Pregunta 46.

Aquí recordamos que $tan\;x=\frac{CO}{CA}$ , es decir que tangente de equis es igual a cateto opuesto sobre cateto adyacente, sabiendo que CO=3 y CA=4, tenemos que $tan\;x=\frac{3}{4}$
Pregunta 45.

Una forma de identificar su naturaleza, es sustituir los coeficientes de la ecuación general en la expresión:
$$A{x^{\bf{2}}} + \;Bxy\; + \;C{y^{\bf{2}}} + \;Dx\; + \;Ey\; + \;F\; = {\bf{0}}$$
$$I=B^2−4AC$$
Que recibe el nombre de invariante o discriminador.
Caso I. B=0
Si 𝐴 = 𝐶 la ecuación representa una circunferencia
Si 𝐴 o 𝐶 = 0 la ecuación representa una parábola
Si 𝐴 ≠ 𝐶 y de signos iguales, la ecuación representa una elipse
Si 𝐴 ≠ 𝐶 y de signos contrarios, la ecuación representa una hipérbola
Caso II. Si 𝐵 ≠ 0
Si $B^2−4AC=0$ la ecuación representa una parábola
Si $B^2−4AC<0$ la ecuación representa una elipse
Si $B^2−4AC>0$. la ecuación representa una hipérbola
Por lo tanto , la ecuación representa una parábola
Pregunta 44.

Recordar la fórmula de Ley de cosenos $a=\sqrt{b^2+c^2-2ab\;cos\;\theta}$ que involucra los tres lados y el un ángulo del triángulo.
Pregunta 43.

La ley de senos nos permite saber un lado si tenemos dos ángulos y otro lado
Pregunta 41.

Del Teorema de Pitágoras, tenemos que de un trángulo rectángulo, siendo a=hipotenusa, b=cateto opuesto y c= cateto adyacente $a^2=b^2+c^2$ y sustituyendo los valores:
$$a^2=b^2+c^2 =(20)^2+(12)^2$$
$$a^2=b^2+c^2 =400+144$$
Despejando la letra a
$$a=\sqrt{544}$$

Se sustituye lo que contenga la función g en la función f, quedando de la siguiente forma la composición de funciones.
$$f(x)=\frac{4}{3[(x-2)^2]^2}$$
Quedando como sigue:
$$f(x)=\frac{4}{3(x-2)^4}$$
Pregunta 39.

El desarrollo del siguiente binomio al cuadrado es:
$${\left( {2{r^3}s – {{{r^2}{s^6}} \over 2}} \right)^2}$$
$$(2{r^3}s)^2 – 2(2{r^3}s){{{r^2}{s^6}} \over 2}+({{r^2}{s^6}\over 2})^2 $$
Desarrollando lo anterior tenemos
$$4r^6s^2-2r^5s^7+\frac{r^4s^{12}}{4}$$
Pregunta 38.

Para resolver el problema, debemos seguir el siguiente proceso.
Primero debemos multiplicar y dividir la ecuación por el coeficiente numérico del término al cuadrado.
$$\frac{2(2x^2+5x-3)}{2}$$
Luego se multiplica arriba y queda así.
$$\frac{(2\cdot{2x^2}+5\cdot{2}\cdot{x}-2\cdot3)}{2}$$
$$\frac{(2x)^2+5(2x)-6}{2}$$
2x hace el papel de la variable y si ven al lado de esa variable hay un 1 como coeficiente y noa ayuda a utilizar el formato siguiente
dos números que sumados den 5 y multiplicados den -6.
quedando de la siguiente forma:
$$\frac{(2x-1)(2x+6)}{2}$$
Ahora solo resta dividir entre 2 uno de los paréntesis del numerador y seleccionamos a (2x+6) por tener número pares
$$(2x-1)\cdot\frac{(2x+6)}{2}$$
quedando lo anterior
$$(2x-1)(x+3)$$
cada factor lo igualamos a cero y depejamos x
$$2x-1=0 \longrightarrow 2x=1 \longrightarrow x=\frac{1}{2}$$
$$x+3=0 \longrightarrow x=-3 $$
Pregunta 37.

Este problema se resueve encontrando dos números que sumados den -1 y esos mismos números multiplicados den -20
Los números son 4 y -5, dado que 4-5=-1 y (4)(-5)=-20
La factorización queda (x+4)(x-5)=0
Y sabemos que x+4=0, despejamos a x y queda x=-4, lo mismo para el otro valor de x, x-5=0,x=5.
Pregunta 36.

Como sabemos $ x^2- y^2=(x+y)(x-y)$ y para nuestro problema tenemos
$\sqrt{4x^2}=2x$ y $\sqrt{1}=1$
Por lo tanto, $ 4x^2- 1=(2x+1)(2x-1)$
Pregunta 35.

Para solucionar este problema, debemos de poner a María como la letra x, así Juan es 2x, por lo tanto, 2x+x=108.
Pregunta 34.

Primero debemos multiplicar por 4 ambos lados de la ecuación, para quitar los denominadores.
$$\left( {{x \over 4} + 1 = {x \over 2}} \right)4$$
Desarrollando lo anterior
$$x + 4 = 2x$$
Despejando equis
$$4 = 2x – x\; \to \;4 = x$$
Nos queda como resultado
$$x = 4$$
Pregunta 33.

Para encontrar el punto P(x,y)dada una razón, tenemos lo siguiente.
$$x=\frac{x_1+x_2r}{1+r}$$ $$y=\frac{y_1+y_2r}{1+r}$$
y sabiendo que la razón es 3 a 1, tenemos que $r=\frac{1}{3}$ y estos datos los sustituimos en las fórmulas anteriores
$$x=\frac{1+0(\frac{1}{3})}{1+\frac{1}{3}}$$
$$y=\frac{-2+3(\frac{1}{3})}{1+\frac{1}{3}}$$
Quedando lo anterior como sigue
$$x=\frac{3}{4}$$
$$y=\frac{-3}{4}$$
Pregunta 32.

La solución es la siguiente:
Primero factorizamos arriba y abajo la ecuación.
$${{{x^2} – 5x + 6} \over {2ax – 6a}}$$
quedando de la siguiente forma:
$${{(x – 2)(x – 3)} \over {2a(x – 3)}}$$
y reduciendo se obtiene
$${{(x – 2)} \over {2a}}$$
Pregunta 31.

Para resolver el problema, debemos plantearlo
x=número y su recíproco es 1/x, por lo tanto queda de la sguiente forma:
$$x+\frac{1}{x}=\frac{41}{20}$$
Multiplicamos ambos lados por 20x
$$\left( {x + {1 \over x} = {{41} \over {20}}} \right)\left( {20x} \right)$$
Desarrollando ambos lados
$$20{x^2} + 20 = 41x$$
Organizando para una forma de ecuación de segundo grado
$$20{x^2} – 41x + 20 = 0$$
Sabiendo que a=20; b=-41; c=20 y sustituyéndola en la fórmula general de segundo grado y resolviéndola.
$${x_{1,2}} = {{ – ( – 41) \pm \sqrt {{{( – 41)}^2} – 4(20)(20)} } \over {2(20)}}$$
$${x_{1,2}} = {{41 \pm \sqrt {1681 – 1600} } \over {40}}$$
$${x_{1,2}} = {{41 \pm \sqrt {81} } \over {40}} = {{41 \pm 9} \over {40}}$$
$${x_1} = {{41 + 9} \over {40}} = {{50} \over {40}} = {5 \over 4}$$
$${x_2} = {{41 – 9} \over {40}} = {{32} \over {40}} = {{16} \over {20}} = {4 \over 5}$$
La respuesta correcta es 5/4 y 4/5.
Pregunta 29.

$${{x – 2} \over {15}} = {{3x – 1} \over 6} – {{2x + 3} \over 5}$$
Multiplicando ambos lados de la ecuación por 30, queda:
$$\left\{ {{{x – 2} \over {15}} = {{3x – 1} \over 6} – {{2x + 3} \over 5}} \right\}30$$
Término a término
$${{30(x – 2)} \over {15}} = {{30(3x – 1)} \over 6} – {{30(2x + 3)} \over 5}$$
desarrollando tenemos:
$$2(x – 2) = 5(3x – 1) – 6(2x + 3)$$
Simplificando
$$2(x – 2) = 5(3x – 1) – 6(2x + 3)$$
$$2x – 4 = 15x – 5 – 12x – 18$$
agrupando en ambos lados:
$$18 – 4 + 5 = 15x – 12x – 2x$$
Despejando:
$$x=19$$
Pregunta 28.

Esta pregunta da como resultado lo siguiente:
$$5a+4(3-7a)=5a+12-28a$$
Simplificando tenemos:
$$12-23a$$
Pregunta 27.

Esta pregunta es el resultado de elevar al cubo un binomio, para esto debes saber que la respuesta correcta es $(a-b)^3=a^3-3a^2b+3ab^2-b^3$
Pregunta 26.

La solución es la siguiente:
$$\frac{x^2y-9xy-36y}{xy-12y}= $$
Factorizando por término común , ariba y abajo.
$$\frac{y(x^2-9x-36)}{y(x-12)}=\frac{x^2-9x-36}{x-12} $$
y se factoriza del resultado anterior la parte de arriba, quedando de la siguiente forma:
$$\frac{(x-12)(x+3)}{x-12} =$$
Simplificando lo anterior
$$=x+3 $$
siendo lo anterior la respuesta correcta
Pregunta 25.

La respuesta correcta es $y=3x+2$, dado que la letra y esta despejada y es única dentro de toda la ecuación.
Pregunta 24.

La ecuación $y=\frac{3x}{x-1}$ se responde despejando la letra x, por lo tanto tenemos:
$$y=\frac{3x}{x-1}\rightarrow y(x-1)=3x \rightarrow xy-y=3x$$
$$xy-3x=y \rightarrow x(y-3)=y$$
despejando x:
$$x=\frac{y}{y-3}$$
Tomando la parte de abajo e igualando a cero tenemos:
$$y-3=0 \rightarrow y=3$$
Concluyendo, la función en su rango admite todos los números reales, excepto al número 3.
Pregunta 23.

Cuando hablamos de polinomios, en este caso un polinomio de primer grado, sabemos que su dominio siempre será en campo de los reales $x\in \mathbb{R}$ o todos los números reales.
Pregunta 22.

El problema es un sistema de ecuaciones con dos incógnitas.
Resolveremos el problema por el método de igualación. Lo primero que debemos hacer es despejar una de las variables, despejaremos la letra x de ambas ecuaciones.
La primera ecuación con x despejada queda:
$$x=\frac{2y+7}{3}$$
La segunda ecuación con x despejada queda:
$$x=\frac{-y+3}{5}$$
Igualando las equis tenemos
$$\frac{2y+7}{3}=\frac{-y+3}{5}$$
Despejando la letra y, resulta:
$$5(2y+7)=3(-y+3)\rightarrow\;10y+35=-3y+9 \rightarrow 10y+3y=-35+9$$
$$13y=-26\rightarrow y=\frac{-26}{13} \rightarrow y=-2$$
Sustituyendo y en $x=\frac{2y+7}{3}$ queda:
$$x=\frac{2(-2)+7}{3} \rightarrow\frac{-4+7}{3}\rightarrow \frac{3}{3}=1$$
El resultado es x=1; y=-2
Pregunta 21.

Para responder esta pregunta , debemos de recordar que la única parte diferente para resolver una desigualdad de una ecuación normal es la de multiplicar por un valor negativo. Una vez hecha la multiplicación, se debe proceder a cambiar la dirección del signo de la desigualdad, es decir cambiar de mayor o igual que a menor o igual que y viceversa.
Por lo tanto la respuesta es $3x \geqslant 16$ multiplicada por -2 queda $ – 6x \leqslant – 32$ al ser multiplicada en ambos lados y cambiando el signo de la desigualdad
Pregunta 20.

Para resolver el anterior problema, debemos de desarrollar la parte de arriba de la fracción $\frac{{{{\left( {x\; + y} \right)}^2} + \;{y^2} + \;2{x^2} – \;15xy}}{x}$ como sigue:
${\left( {x\; + y} \right)^2} + \;{y^2} + \;2{x^2} – \;15xy = {x^2}\; + 2xy + {y^2} + \;{y^2} + \;2{x^2} – \;15xy$
reduciendo términos queda
$$ = 3{x^2} + 2xy + 2{y^2} – 15xy = 3{x^2} – 13xy + 2{y^2}$$
por último, dividiendo término a término entre x nos da lo siguiente:
$$\frac{{3{x^2} – 13xy + 2{y^2}}}{x} = 3x – 13y + \frac{{2{y^2}}}{x}$$
Pregunta 19.

Para resolver la pregunta se debe aplicar la operación de los radicales siguiente $\sqrt[n]{ab}=\sqrt[n]{a}\sqrt[n]{b}$
Lo anterior aplicado a nuestro ejercicio quedaría de la siguiente forma:
$\sqrt{3x} \sqrt{6x+3} = \sqrt{(3x)(6x+3)}$
haciendo la multiplicación
$\sqrt{18x^2+9x}$ y factorizando lo de adentro del radical queda: $\sqrt{9(2x^2+x}=\sqrt{9}\sqrt{2x^2+x}= 3\sqrt{2x^2+x} $
Pregunta 18.

Para resolver el problema 18 se tiene que recordar las propiedades de los radicales que cumplen con la regla de exponentes. Para esto hay que ver que $\sqrt[n]{x^m}=x^{m/n}$
Para nuestro problema tenemos $\sqrt{3x^2+6}+\sqrt{(7x+3)^3}$, quedando de la siguiente forma $(3x^2+6)^{1/2}+(7x+3)^{3/2}$
Pregunta 17.

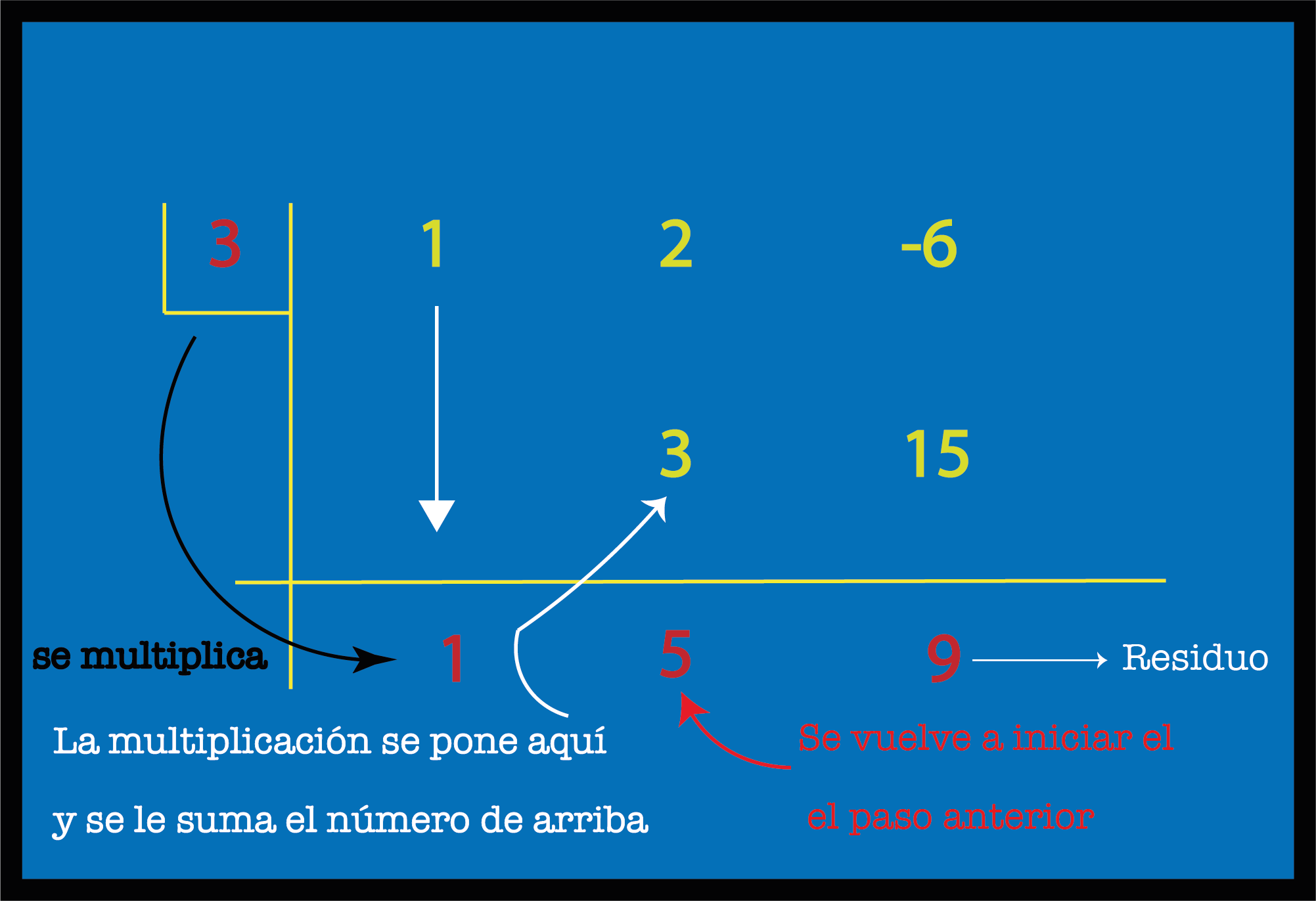
Para determinar el residuo de un polinomio con un binomio lineal, es necesario recurrir a la división sintética de polinomios.
Dividir $x^2+2x-6$ con $x-3$ primero se despeja del divisor la letra x, quedando de la siguiente forma $x=3$ y ese número se pone en la rejilla de división sintética.